GeoTeric’s standard Frequency Decomposition contains two key options, Constant Bandwidth and Constant Q. These two options control the relationship between the central frequency, bandwidth, scale and modulation of the filters applied.
Gabor wavelets are the complex time-localised functions which are used in GeoTeric's Frequency Decomposition to extract information about the frequency content of seismic signals. Gabor wavelets are used because their shape corresponds closely to that of events in seismic reflectivity data and they have very good joint time-frequency resolution.
Scale - the length (width) of the Gabor wavelet
Frequency - the number of cycles in the underlying Sine wave over a fixed length of signal (defined by the scale).
Modulation - The factor determining the frequency of the Sine/Cos complex modulation function.
Bandwidth - The difference between the upper and lower cut-off frequencies of a filter. In GeoTeric, this is set to include 98% of the total power of the Gabor wavelet.
There is an inverse relationship between scale and frequency (when the modulation is constant), so low frequencies with a modulation of 1 will need a larger scale filter than high frequencies with a modulation of 1 which will need a small scale filter.
Likewise, there is an inverse relationship between scale and bandwidth (when the frequency is constant), so a given frequency with a small bandwidth will need a higher scale filter than the same frequency with a wide bandwidth which will need a smaller scale filter.
The Constant Bandwidth method uses a constant filter length and a constant bandwidth (the modulation increases with increasing frequency to maintain the bandwidth and scale, Fig.1). This means it has good frequency resolution as the bandwidth is low, however the filter size is set to the size required for the lowest frequency, so the vertical resolution of the output volumes is poor and the magnitude volumes often appear smeared in the vertical domain.
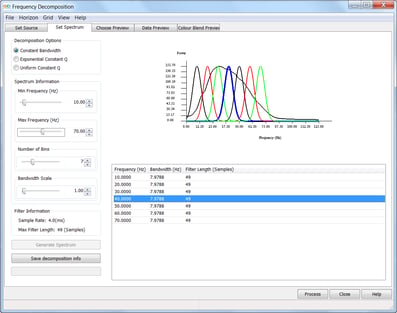
Figure 1. Constant Bandwidth filters
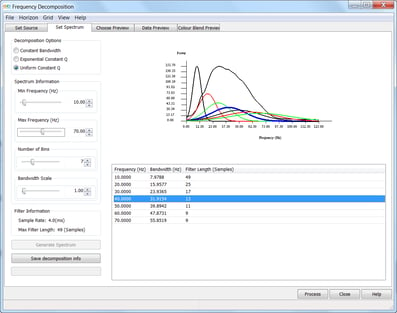
Figure 2. Constant Q filters
HD Frequency Decomposition (HDFD) uses a modified matching pursuit algorithm which matches a bank of Gabor wavelets to each event in the data. This results in very high vertical resolution (the same resolution as the input data), but poor frequency resolution (as the bandwidths are very wide to enable the good vertical resolution).
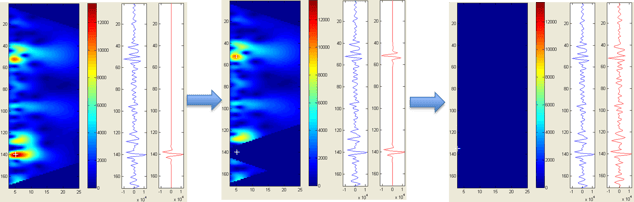
Figure 3. HD Frequency Decomposition process
Please check back soon for part 2 of this blog post, in which we discuss which techniques are best applied in different scenarios.

